Домен{*область*}
AutoCAD solids - контурные представления (часто упоминаемый как B-rep модели), состоят из коллекции топологических объектов связности и связал геометрические граничные объекты. Топологические объекты определены в AcBr библиотеке и описаны позже в этой главе, принимая во внимание, что геометрические объекты определены в AcGe библиотеке.
Объекты, определенные или сгенерированные AcBr библиотекой постоянно находятся в трехмерном Евклидовом пространстве модели (E 3). Единственные исключения - геометрические объекты, определенные в двумерном пространстве{*пробеле*} параметра поверхности (типа кривых параметра и значений параметра).
Вообще, только 2-разнообразный топологический домен{*область*} поддержан AcBr библиотекой. Особенности (которые являются геометрическими вырождениями) поддержаны, чтобы представить вершину конуса, но проводных тел и смешанной размерности solids (который может включать повисшие провода, и лица) не поддержаны; и при этом они не могут быть реализованы в AutoCAD.
Общий неразнообразный домен{*область*} - надмножество 2-разнообразного домена{*области*}, и позволяет отличным твердым объемам касаться в единственных{*отдельных*} точках, кривых, или лицах; и позволяет любую комбинацию каркаса, листа, и твердых объектов. Следующие неразнообразные объекты поддержаны в соответствии с AutoCAD и AcBr библиотекой:
§
Два 2-разнообразного solids, объединенный по общедоступному краю или вершине
§ объект AcDbBody, содержащий единственное лицо
Топологический объект может быть неограничен (то есть это не может иметь никакой более низкой размерной топологии ограничения) только в следующих случаях:
§ замкнутая поверхность, которая свойственно ограничена, и в u и v руководствах{*направлениях*} (типа полного тора или сферы), представлен лицом, которое не имеет никаких границ цикла.
§ замкнутая кривая, которая свойственно ограничена (типа полного круга или эллипса), представлен краем, который имеет совпадающее начало и конечную вершину.
Ограничения
Некоторые операции не могут поддерживать неоднородное масштабирование. Это включает все функции, которые возвращают внешнюю кривую или поверхность (включая поверхности НЕОДНОРОДНОГО РАЦИОНАЛЬНОГО В-СПЛАЙНА).
Полная цепочка трансформант от пути подпримитива кэшируется во время этого, путь подпримитива объекта AcBr установлен (по причинам эффективности). Если блок-ссылка перемещена, это укажет на новую матрицу трансформант, но объект AcBr не будет знать, что его кэшируемая трансформанта устаревшая. Если вставка изменена, чтобы обратиться к различному примитиву AutoCAD, путь подпримитива просто больше не имеет уместность и должен быть модифицирован, чтобы отразить новую ссылку примитива перед использованием, чтобы повторно инициализировать все уместные объекты AcBr.
Особенности (типа вершины конуса) карта к граням в AutoCAD и таким образом может использоваться, чтобы инициализировать AcBrEdge для специальной цели запроса для вершины, но нельзя делать запрос для геометрии кривой или использоваться, чтобы установить AcBrLoopEdgeTraverser. К ним можно также обращаться, используя AcBrLoopVertexTraverser, поскольку особенность соответствует единственной границе цикла лица.
Также, как с указателями AcDbObject, объекты AcBr не могут использоваться, как только объект базы данных AutoCAD был закрыт в базе данных или идет из контекста; они не постоянны. Любое изменение к объекту базы данных будет помечено как eBrepChanged ошибка, если уровень проверок правильности не был установлен, чтобы игнорировать изменения базы данных. Из-контекста или закрытого объекта базы данных будет вообще заставлять Acad:: eNotInDatabase быть возвращенным.
Иерархия Классов
AcBr иерархия классов - подмножество ObjectARX иерархии классов, и определяет следующие классы:
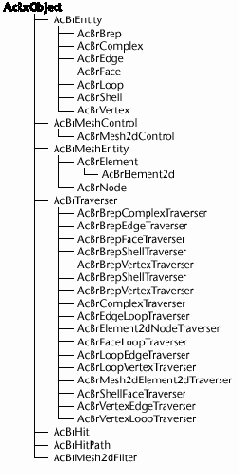
Обратите внимание, что объекты AcBr не получены из AcDbObject, и поэтому не могут быть зарегистрированы с базой данных AutoCAD.
