Контекст примитива и координатное преобразовывание данных
AcedNEntSelP () функция подобна acedEntSel (), за исключением того, что это передает два дополнительных параметра результата, чтобы облегчить обработку примитивов, которые вложены в пределах блок-ссылок.
ОБРАТИТЕ ВНИМАНИЕ На другое различие между acedNEntSelP () и acedEntSel () - то, что, когда пользователь отвечает на acedNEntSelP () запрос, выбирая сложный примитив, acedNEntSelP () возвращает выбранный подпримитив а не, заголовок сложного примитива как acedEntSel () делает. Например, когда пользователь выбирает ломаную линию, acedNEntSelP () возвращает подпримитив вершины вместо заголовка ломаной линии. Чтобы восстановить{*отыскивать*} заголовок ломаной линии, приложение должно использовать acdbEntNext () чтобы идти вперед к Seqend подпримитиву и получать имя заголовка от -2 группы Seqend подпримитива. Это истинно также, когда пользователь выбирает атрибуты во вложенной блок-ссылке и когда точка указки определена в acedNEntSelP () запрос.
Координатное Преобразование
Первый из дополнительных параметров, возвращенных acedNEntSelP () - 4x4 матрица преобразования типа ads_matrix. Эта матрица известна как Модель к Мировой Матрице преобразования. Это дает возможность приложению преобразовать точки в данные определения примитива (и расширенные{*продленные*} данные, если это присутствует) от образцовой системы координат примитива (MCS) в Мировую систему координат (WCS). MCS применяется{*обращается*} только к вложенным примитивам. Начало координат MCS - точка вставки блока, и его ориентация - таковой ВЕРХНИХ РЕГИСТРОВ, который был в действительности, когда блок был создан.
Если выбранный примитив - не, вложенный примитив, матрица преобразования установлен в единичную матрицу. Преобразование выражено следующим матричным умножением:
Индивидуальные координаты преобразованной точки получены от уравнений, где М. mn - Модель к Мировой Матрице преобразования, координирует, (X, Y, Z) - точка данных определения примитива, выраженная в координатах MCS, и (X ’, Y ’, Z ’) - заканчивающаяся точка данных определения примитива, выраженная в координатах WCS. См. “ Матрицы Преобразования ” на странице 535.
ПРИМЕЧАНИЕ, чтобы преобразовать вектор скорее чем точка, не добавьте вектор сдвига [М. 03 М. 13 М. 23] (от четвертого столбца матрицы преобразования).
Следующий типовой код определяет функцию, mcs2wcs (), который исполняет преобразования, описанные предшествующими уравнениями. Требуется матрица преобразования, возвращенная acedNEntSelP () и одиночной точкой (возможно от данных определения вложенного примитива), и возвращает оттранслированную точку.
Если третий параметр к mcs2wcs (), is_pt, установлен в 0 (ЛЖИ), последний{*прошлый*} столбец матрицы преобразования — вектор сдвига, или смещение — не добавлено к результату. Это дает возможность функции транслировать вектор также как точку.
|
X ’ |
М00 М01 М02 М03 |
X |
||
|
Y ’ |
= |
М10 М11 М12 М13 |
x |
Y |
|
Z ’ |
М20 М21 М22 М23 |
Z |
||
|
1.0 |
0.0 0.0 0.0 1.0 |
|
1.0 |
X ' = М. 00 X + М. 01 Y + М. 02 Z + М. 03
Y ' = М. 10 X + М. 11 Y + М. 12 Z + М. 13
Z ' = М. 20 X + М. 21 Y + М. 22 Z + М. 23.
Индивидуальные координаты преобразованной точки получены от уравнений, где М. mn - Модель к Мировой Матрице преобразования, координирует, (X, Y, Z) - точка данных определения примитива, выраженная в координатах MCS, и (X ’, Y ’, Z ’) - заканчивающаяся точка данных определения примитива, выраженная в координатах WCS. См. “ Матрицы Преобразования ” на странице 535.
ПРИМЕЧАНИЕ, чтобы преобразовать вектор скорее чем точка, не добавьте вектор сдвига [М. 03 М. 13 М. 23] (от четвертого столбца матрицы преобразования).
Следующий типовой код определяет функцию, mcs2wcs (), который исполняет преобразования, описанные предшествующими уравнениями. Требуется матрица преобразования, возвращенная acedNEntSelP () и одиночной точкой (возможно от данных определения вложенного примитива), и возвращает оттранслированную точку.
Если третий параметр к mcs2wcs (), is_pt, установлен в 0 (ЛЖИ), последний столбец матрицы преобразования — вектор сдвига, или смещение — не добавлено к результату. Это дает возможность функции транслировать вектор также как точку.
void mcs2wcs(xform, entpt, is_pt, worldpt)
ads_matrix xform;
ads_point entpt, worldpt;
int is_pt;
{
int i, j;
worldpt[X] = worldpt[Y] = worldpt[Z] = 0.0;
for (i=X; i<=Z; i++)
for (j=X; j<=Z; j++)
worldpt[i] += xform[i][j] * entpt[j];
if (is_pt) // If it’s a point, add in the displacement
for (i=X; i<=Z; i++)
worldpt[i] += xform[i][T];
}
Следующий кодовый фрагмент показывает, как mcs2wcs () мог бы использоваться в конъюнкции с acedNEntSelP () чтобы транслировать значения точки в поток WCS.
ads_name usrent, containent;
ads_point usrpt, defpt, wcspt;
ads_matrix matrix;
struct resbuf *containers, *data, *rb, *prevrb;
status = acedNEntSelP(NULL, usrent, usrpt, FALSE, matrix,
&containers);
if ((status != RTNORM) || (containers == NULL))
return BAD;
data = acdbEntGet(usrent);
// Extract a point (defpt) from the data obtained by calling
// acdbEntGet() for the selected kind of entity.
.
.
.
mcs2wcs(matrix, defpt, TRUE, wcspt);
AcedNEntSelP () функция также позволяет программе определять точку указки. Pickflag параметр определяет, действительно ли acedNEntSelP () называется в интерактивном режиме.
В следующем примере, acedNEntSelP () запрос определяет его собственную точку для выбора примитива и не запрашивает пользователя. Pickflag параметр ИСТИНЕН, чтобы указать, что запрос поставляет{*снабжает*} его собственному значению точки (также, подсказка - NULL).
ads_point ownpoint;
ownpoint[X] = 2.7; ownpoint[Y] = 1.5; ownpoint[Z] = 0.0;
status = acedNEntSelP(NULL, usrent, ownpt, TRUE, matrix, &containers);
AcedNEntSel () функция обеспечивается для совместимости с существующими ObjectARX-приложениями. Новые приложения должны быть написаны, используя acedNEntSelP ().
Модель к Мировой Матрице преобразования, возвращенной запросом к acedNEntSel () имеет ту же самую цель как возвращенное acedNEntSelP (), но это - 4x3, матрица — прошла как массив четырех точек —, который использует соглашение, что точка - строка скорее чем столбец. Преобразование описано следующим матричным умножением:
|
М00 М01 М02 М03 |
|
|
X' Y' Z' 1.0 = X Y Z 1.0 x |
М10 М11 М12 М13 |
|
М20 М21 М22 М23 |
|
|
0.0 0.0 0.0 1.0 |
void mcs2wcs(xform, entpt, is_pt, worldpt);
ads_point xform[4]; // 4x3 version
ads_point entpt, worldpt;
int is_pt;
Форма тождества 4x3 матрица следующие:
|
1 0 0 |
|
0 1 0 |
|
0 0 1 |
|
0 0 0 |
Контекстные Данные
Функция acedNEntSelP () обеспечивает параметр для контекстных данных, refstkres. (Это - другая особенность, не обеспеченная acedEntSel ()). Refstkres параметр - указатель на список связей буферов результатов, который содержит названия{*имена*} контейнерных блоков примитива. Список заказывается{*упорядочивает*} от самого низкого до самого высокого. Другими словами, имя в списке - имя блока, содержащего выбранный примитив, и фамилия в списке - имя блока, который был непосредственно вставлен в рисунок. Следующий рисунок показывает формат этого списка.
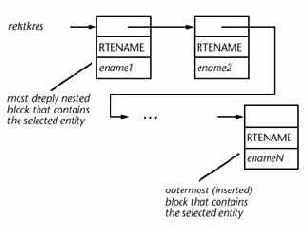
Если выбранный примитив entres - не, вложенный примитив, refstkres - указатель NULL. Это - удобный способ проверить, действительно ли координаты примитива должны быть оттранслированы. (Поскольку xformres возвращен как единичная матрица для примитивов, которые не вложены, применяя это к координатам таких примитивов не никакой вред, но стоит некоторое бесполезное время выполнения.)
Используя объявления от предыдущего acedNEntSelP () пример, имя блока, который немедленно содержит выбранный пользователем примитив, может быть найден следующим кодом (в acedNEntSelP () запрос, pickflag параметр - FALSE для интерактивного выбора).
status = acedNEntSelP(NULL, usrent, usrpt, FALSE, matrix,
&containers);
if ((status != RTNORM) || (containers == NULL))
return BAD;
containent[0] = containers->resval.rlname[0];
containent[1] = containers->resval.rlname[1];
Имя наиболее удаленного контейнера ( то есть примитив, первоначально вставленный в рисунок) может быть найдено последовательностью типа следующего:
// Проверить это, контейнеры не уже NULL.
rb = containers;
while (rb != NULL) {
prevrb = rb;
rb = containers->rbnext;
}
// Буфер результатов, указанный prevrb теперь содержит имя наиболее удаленного блока.
В следующем примере, текущая система координат - WCS. Использование AutoCAD, создайте блок по имени КВАДРАТ, состоящий из четырех линий.
Command: line
From point: 1,1
To point: 3,1
To point: 3,3
To point: 1,3
To point: c
Command: block
Block name (or ?): square
Insertion base point: 2,2
Select objects: Select the four lines you just drew
Select objects: ENTER
Тогда вставьте блок в UCS, вращал 45 градусов относительно Z оси.
Command: ucs
Origin/ZAxis/3point/Entity/View/X/Y/Z/Prev/Restore/Save/Del/?/
<World>: z
Rotation angle about Z axis <0>: 45
Command: insert
Block name (or ?): square
Insertion point: 7,0
X scale factor <1> / Corner / XYZ: ENTER
Y scale factor (default=X): ENTER
Rotation angle: ENTER
Если ObjectARX-приложение вызывает acedNEntSelP () (или acedNEntSel ()) и
пользователь выбирает левую нижнюю сторону квадрата, эти функции заставляют entres параметр равняться имени выбранной линии. Они устанавливают точку указки (ptres) в (6.46616, -1.0606,0.0) или близлежащее значение точки. Они возвращают матрицу преобразования (xformres) как показано в следующем рисунке.
Наконец, они заставляют список контейнерных примитивов (refstkres) направлять на одиночный буфер результатов содержащий имени примитива блока SQUARE.
|
0.707107 |
-0.707107 |
0.0 |
4.94975 |
0.707107 |
0.707107 |
0.0 |
|
|
0.707107 |
0.707107 |
-0.0 |
4.94975 |
-0.707107 |
0.707107 |
0.0 |
|
|
0.0 |
0.0 |
1.0 |
0.0 |
0.0 |
-0.0 |
1.0 |
|
|
0.0 |
0.0 |
0.0 |
1.0 |
4.94975 |
4.94975 |
0.0 |
